After years of development, the first Crew Dragon reached the International Space Station on Sunday (this spacecraft is gorgeous!) and is coming back to land tomorrow, off the coast of Florida. Discussing the reentry on twitter with a couple of folks yesterday, I came across an interesting question: do we know how long before splashdown Dragon will fly over which parts of the world?
If you work at SpaceX or NASA, the answer is (I hope) yes. Since I don’t work for either, I spent the evening trying to program a (simplistic) reentry simulation to find out for myself. I’d done that years ago but the physics and code were pretty appalling, so I started from scratch.
Reentry is a relatively simple problem to solve as long as you don’t look at the details. There are either two or three forces acting on the spacecraft: gravity, aerodynamic drag, and in the case of Dragon – or really most modern spacecrafts since the introduction of Soyuz – lift. There are simplified equations for all of these, which I used to derive equations of motion, coded into a quick-and-dirty Euler solver.
There are major issues with this, obviously. Aerodynamic parameters for a spacecraft are both complex – you go from hypersonic flight in plasma to subsonic flight under parachutes – and not exactly published in great details. The lift and drag equations I use are also not all that good in very-low-density gases, which is where spacecrafts spend a good chunk of their reentries.
Still, I came up with some trajectories and g-loads that look pretty close to what you’d expect. Lifting reentries to low earth orbit are usually between 3G and 5G (Trevino 2008), which we have here. We can see an upwards bend in the trajectory when lift starts to be significant, and it takes the capsule about 8 minutes to go from Entry Interface to parachute deployment, which matches the timeline obtained by NASASpaceFlight nicely!
I also made a plot that shows how far dragon will be from splashdown compared to the time left before it gets there. Bear in mind, the simulation stops when the parachute would open, so it’s not very precise – Dragon will probably drift due to winds – and needs a couple of minutes added onto the timeline to get to the predicted splashdown time.
What if we tried more spacecrafts?
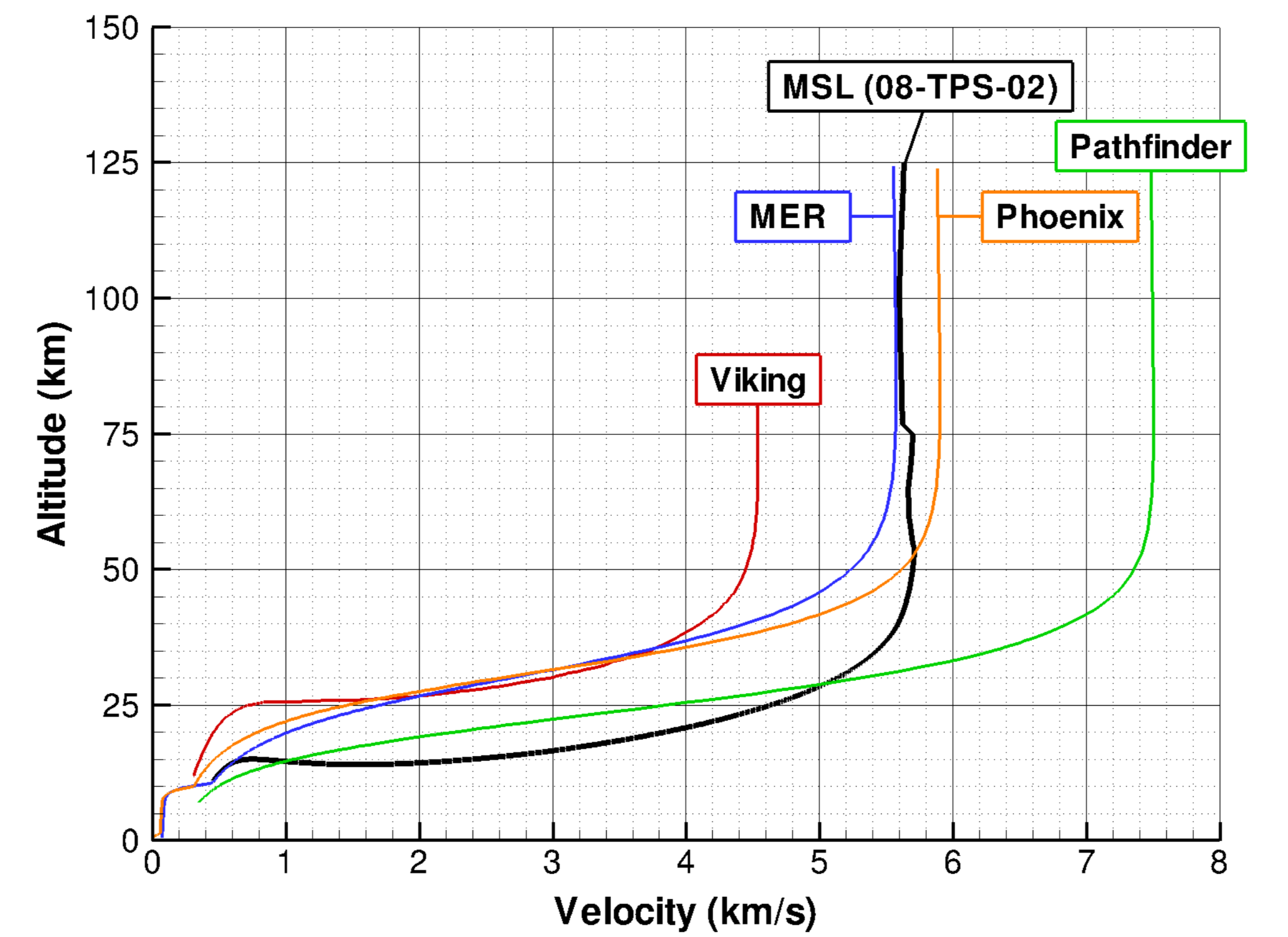
Since I specialise in taking things too far, I tried to find aerodynamic data for more spacecrafts and planets. It turns out you can find a lot of information on NASA’s Mars missions, so I tried to plot reentries for Pathfinder, Opportunity and Curiosity. The results are surprisingly okay! Not stellar, but also not too far off compared to a plot found in (Edquist et al. 2009), which is more than I expected given the small amount of time I spent working on this!
Curiosity’s profile is probably the one that’s further off, and it makes sense. Of those three missions, it’s the only one that used body lift to control its entry. In my simulations, that lift is pointed up the whole time, whereas the real mission rolled around to steer and control the descent. As a bonus, I added the now-cancelled Red Dragon’s entry, thought it’s also probably way off. Had it happened, the plan for the mission was to point the lift downwards (!) to reach the thicker layers of the atmosphere, then modulate it to achieve level-ish flight and shed speed there, instead of skipping back up like it does in my sims.
Realistically, these kind of simulations don’t have a lot of value in terms of real-life applications – you won’t design a mission with one single dirty python script. But they’re the kind of things I love spending some time doing once in a while, because they show that first principles are still a good way to get an idea of what a problem looks like. That, and saying that you can (sort of) simulate the next Crew Dragon reentry on your laptop gets you a bunch of cool points 🚶🏻♀️🚀
Source Code
I coded all of this using Python 3, and Matplotlib for plotting. You can get the source from GitHub at amyinorbit/reentry.py. It’s under the MIT license, so feel free to hack it and make changes to it! There’s tonnes that could be done – adding more planets, using a more robust solver, etc.
Papers I read & used
- Trevino, Loretta. SpaceX Dragon Re-Entry Vehicle: Aerodynamics and Aerothermodynamics with Application to Base Heat-Shield Design. Georgia Institute of Technology, 2008.
- Karcz, John, et al. Red dragon: Low-cost access to the surface of mars using commercial capabilities. 2012.
- Edquist, Karl, et al. Aerothermodynamic design of the Mars Science Laboratory heatshield. 41st AIAA Thermophysics Conference. 2009.




